2021GDUFS新手赛D-DUNE 题解

题面

题目背景

这个沙漠星球，我们称之为厄拉科斯（Arrakis）。

而它的原住民称其母星为沙丘（Dune）。

厄拉科斯在繁星的映衬下逐渐出现：一个沙漠世界。

一股巨大的铁锈色沙暴飓风正在厄拉科斯的赤道上缓慢地移动。
一艘隐形飞船驾向厄拉科斯大地：造型奇异的双座工具，完全光滑，深黑，没有标志……

厄崔迪家族从哈克南家族手中接过了厄拉科斯的统治权,现在正是将所有物资运往厄拉科斯的关键时刻.厄崔迪男爵不想出任何问题,于是委托你——厄崔迪家族的首席飞船调度员,来安排飞船的航线.

题目描述

你要安排的航线系统可以表示成一个二维的平面图.你的飞船调度室在$(0,0)$.从西到东,从南到北各有100条航道.不同的运输飞船会同时从各个航道的起点,可以表示为$(0,i)$或$(j,0)$ $(1<=i<=100,1<=j<=100)$以相同速度起飞,现在有n架从西到东和m架从南到北的飞船,(每条航道上最多只能有一架飞船),在保证所有飞船都不相撞的情况下,想要运输最多的物资——也就是让能同时起飞的飞船最多.你想知道具体能最多让多少架飞船同时起飞?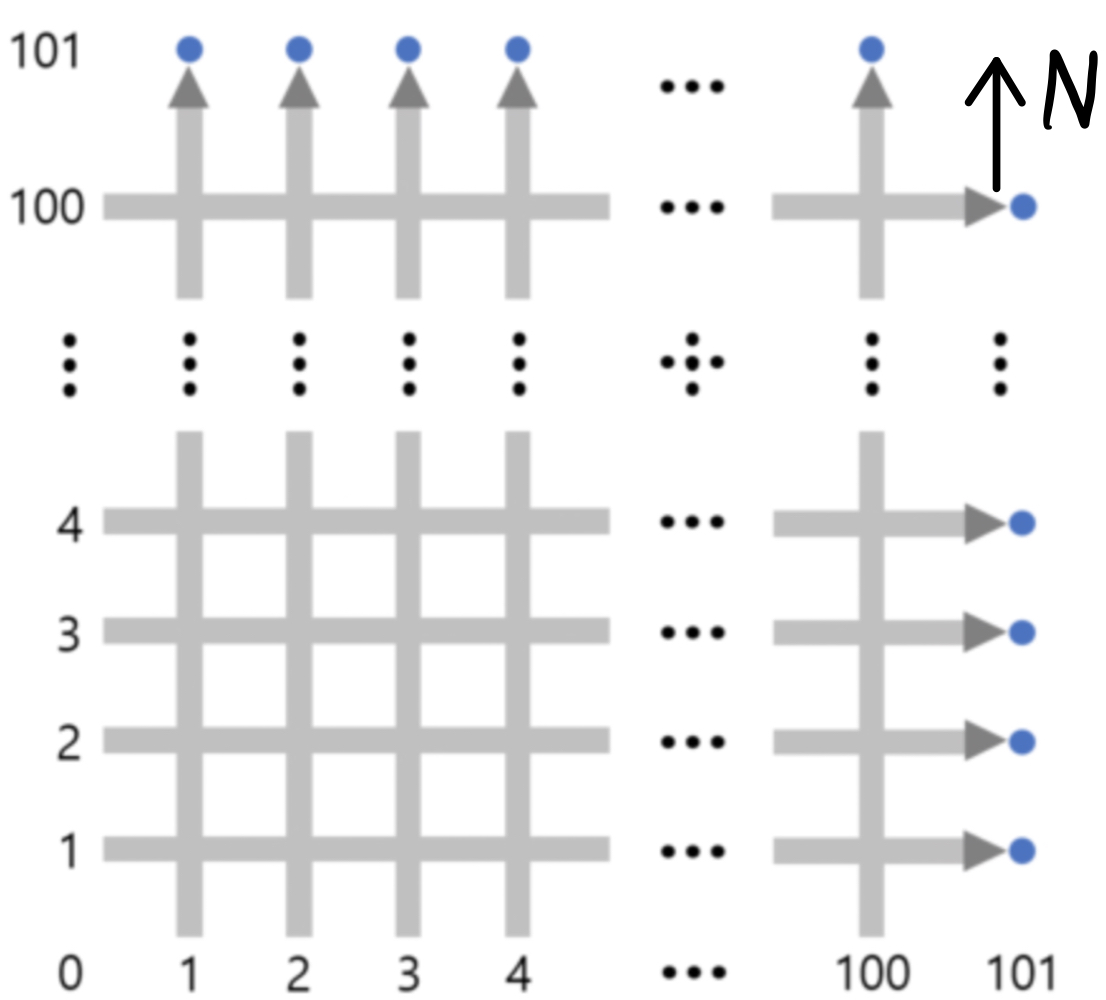

输入格式

第一行输入一个整数$n(1<=n<=100)$和一个整数$m(1<=m<=100)$,表示$n$架从西向东和$m$架从南面向北的飞船,第二行输入$n$个飞船分别起飞的航道,第三行输入$m$个飞船分别起飞的航道.(保证输入的每一条航道上只有一个飞船)

输出格式

输出一个整数,表示最多可以保留的飞船数.

题解

  • 注意到所有飞船都是相同速度，那么$X_{i}$会和$Y_j$航道上的飞船当且仅当$i=j$。所以只要统计所有$i=j$的情况，减去任意一艘，最后就是答案。
  • $O(n^2)$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;
const int M = 1e5 + 5;
const ll INF = 0x3f3f3f3f3f3f3f3f;
const ll mod = 1e9 + 7;
void solve()
{
    int n, m, i, j;
    cin >> n >> m;
    bool v[105] = { 0 };
    int ans = 0;

    for (i = 0; i < n; i++)
    {
        int x;
        cin >> x;
        v[x] = true;
    }
    for (i = 0; i < m; i++)
    {
        int x;
        cin >> x;
        if (v[x])
            ans++;
    }
    cout << n+m-ans;
}

int main() {
   
    int T = 1;
    for (int cas = 1; cas <= T; cas++) {
        solve();
    }

    return 0;
}

  • $O(n)$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#include<bits/stdc++.h>
using namespace std;

const int N = 110;

int n, m, a[N];

int main(){
	scanf("%d %d", &n, &m);
	int x, ans = 0;
	for(int i=1; i<=n; ++i){
		scanf("%d", &x);
		a[x]=1;
    ans++;
	}
	for(int i=1; i<=m; ++i){
		scanf("%d", &x);
		if(a[x] != 1)ans++;
	}
	printf("%d\n", ans);

	return 0;

}